In computer graphics we often need to be able to display a three-dimensional image in two dimensions and preserve the perspective appearance. If we walk on a straight road, it appears that the road narrows with the distance. This is the perspective effect and it is a result of mapping a three-dimensional image on a two-dimensional surface (i.e. a computer monitor, a screen, or the retina of the eye).
This tutorial is not about stereoscopic view, which refers to a technique for enhancing the illusion of depth in an image by presenting two offset images separately to the left and right eye of the viewer.
3D Perspective Conversion in Excel – Part #1
– by George Lungu
In computer graphics we often need to be able to display a three-dimensional
image in two dimensions and preserve the perspective appearance. If we walk on a
straight road, it appears that the road narrows with the distance.
This is the perspective effect and it is a result of mapping a three-dimensional image on a two-
dimensional surface (i.e. a computer monitor, a screen, or the retina of the eye).
This tutorial is not about stereoscopic view, which refers to a technique for
enhancing the illusion of depth in an image by presenting two offset images separately
to the left and right eye of the viewer.
<excelunusual.com> 1
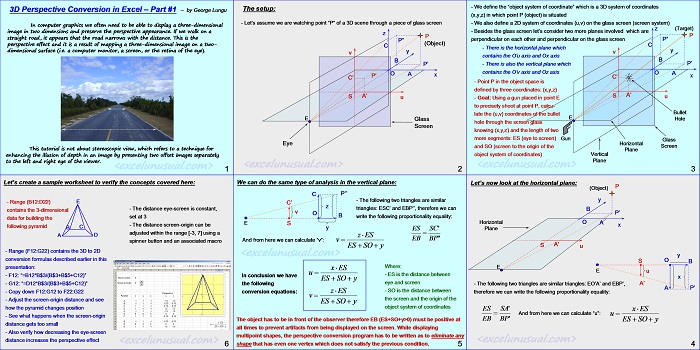
The setup:
– Let’s assume we are watching point “P” of a 3D scene through a piece of glass screen
(Object)
O A x
E Glass
Screen
Eye
<excelunusual.com> 2
– We define the “object system of coordinate” which is a 3D system of coordinates (x,y,z) in which point P (object) is situated
– We also define a 2D system of coordinates (u,v) on the glass screen (screen system) z (Target)
– Besides the glass screen let’s consider two more planes involved which are perpendicular on each other and perpendicular on the glass screen
– There is the horizontal plane which contains the O’u axis and Ox axis
– There is also the vertical plane which P’ contains the O’v axis and Oz axis
– Point P in the object space is defined by three coordinates: (x,y,z)
– Goal: Using a gun placed in point E u to precisely shoot at point P, calculate the (u,v) coordinates of the bullet
hole through the screen glass knowing (x,y,z) and the length of two more segments: ES (eye to screen)
and SO (screen to the origin of the Screen object system of coordinates) Vertical
Bullet Hole
Gun
Glass
Horizontal
Plane
eye and screen
<excelunusual.com> 3
Let’s now look at the horizontal plane:
(Object)
y, B, P’
Horizontal O A
x, Plane
– The following two triangles are similar triangles: EO’A’ and EBP’, A’A P’ therefore we can write the following proportionality equality:
ES SA’ x ES
And from here we can calculate “u”:
We can do the same type of analysis in the vertical plane:
C P’’
– The following two triangles are similar triangles: ESC’ and EBP’’, therefore we can write the following proportionality equality:
And from here we can calculate “v”: EB BP”
Where:
xES
– ES is the distance between
In conclusion we have the following conversion equations:
ES =SO* y
Where:
-ES is the distance between eye and screen
-SO is the distance between the screen and the origin of the object system of coordinates
The object has to be in front of the observer therefore EB (ES+SO+y>0) must be positive at
all times to prevent artifacts from being displayed on the screen.
While displaying multi-point shapes, the perspective conversion program has to be written as to
eliminate any shape that has even one vertex which does not satisfy the previous condition.
<excelunusual.com> 5
Let’s create a sample worksheet to verify the concepts covered here:
-Range (B12:D22) contains the 3-dimensional data for building the following pyramid:
-The distance eye-screen is constant, set at 3
-The distance screen-origin can be adjusted within the range [-3, 7] using a spinner button and an associated macro
– Range (F12:G22) contains the 3D to 2D conversion formulas described earlier in this presentation:
– F12: “=B12*B$3/(B$3+B$5+C12)”
– G12: “=D12*B$3/(B$3+B$5+C12)”
– Copy down F12:G12 to F22:G22
– Adjust the screen-origin distance and see how the pyramid changes position
– See what happens when the screen-origin distance gets too small
– Also verify how decreasing the eye-screen distance increases the perspective effect
by George Lungu <excelunusual.com>