After learning how to model ideal logic gates in MS Excel 2003 it is time to attemp to create a delay based model.
This first model is just a theoretical presentation about delay, how it can be explained and how it can be modeled with a minimum amount of formulas while keeping a reasonable precision.
The presentation focuses on the basic CMOS inverter and it shows that for a basic single-stage logic gate the delay is mainly driven by the product between an equivalent Thevenin output impedance and the capacitance seen at the output of the gate, which obviously includes the input capacitance of the following stage and perhaps the transmission line capacitance.
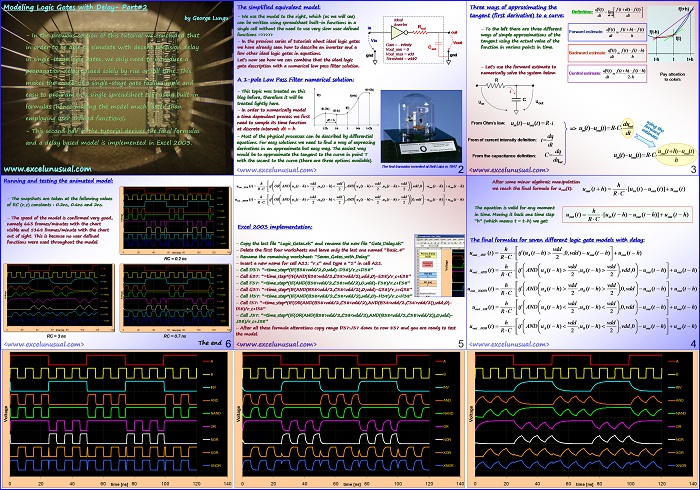
Modeling Logic Gates with Delay- Part#1
by George Lungu
– The previous series of tutorials treated logic gates ideally without considering
propagation delays, having perfect edges at the output (negligible rise time and fall time)
and with infinite voltage gain (the gate fully switches for the slightest deviation of the
input voltage around a threshold – typically vdd/2).
– The purpose of the models developed on this blog is not only educational but also
utilitarian. We therefore try to obtain interactive and animated models which are targeted
to be fairly fast. While modeling a gate with all the aforementioned effects is fairly trivial
in Excel (especially by using user defined functions), the model would become slow when
these said models were to involve more than a half of dozen gates (as we could see in one
of the previous tutorials about ideal logic gates).
– In order to be able to conveniently simulate effects such as glitches in combinatorial logic
(static and dynamic hazard), oscillation in ring and relaxation oscillators, etc, with
reasonable precision, we only need to introduce a propagation delay caused solely by rise
or fall time (we actually consolidate propagation delay and edge delays in a single effect
since we will apply the model to single-stage gates).
This makes the model of a single-stage gate fairly simple and easy to program in a single cell using built-in spreadsheet formulas
(hence making the model much faster than using user defined functions).
The delay mechanism in single-stage logic gates:
– Let’s consider the schematic of a isolated inverter used in the design of an integrated circuit digital
block and then let’s connect it with other logic gates and see how we can model delays.
-Let’s also include the parasitic capacitances which cause rise time and fall time delays. For any given
logic gate the capacitance at the input of a gate is usually higher than its capacitance at its own
output. The total capacitance at a logic gate output connected in a circuit is the sum between it’s own
output capacitance and the input capacitance into the next stage (the latter usually dominates).
vdd vdd
PMOS (pull up
in transistor) out in out
NMOS (pull down transistor)
Co1 Ci2 Co2 Ci3
gnd
Driving gate
Current gate Driven gate
(some arbitrary configuration) vdd
-Let’s now consolidate a node capacitance into a total capacitance “Ct” and attribute it to a the output of the driving gate Co1+Ci2
Driving gate
Current gate Driven gate
<excelunusual.com>
2
A Thevenin equivalent of a single-stage logic gate (inverter):
– After we consolidated the capacitances on each node, let’s see how we can model an inverter using a
Thevenin approximation.
– Without getting into details you can read about Thevenin’s theorem and Thevenin equivalent circuits:
– Besides the input capacitance, the input of the inverter (or some other logic gate) has a very high impedance
since the input node is composed of two transistor gates which are isolated from the rest of the circuit.
– The output can be modeled by a voltage source and a series resistor. Looking at the static characteristic of an
inverter (the ones below were published by professor Bruce McNair from Stevens Institute of Technology –
bmcnair@stevens-tech.edu) we can see that for a typical gate the maximum gain (when output is around vdd/2
where both NMOS and PMOS transistors are in saturation) is around the value of -20 (negative). The crowbar
(short circuit) current for a small gate in the modern CMOS process is about 5uA -20uA around 2V supply
which gives typical output resistances in the
range of hundreds of KW.
– The values above are rough approximations. Besides, a CMOS
logic gate has a Thevenin small signal output resistance that
varies wildly depending on the large signal value of the output
(the transistors can be either in a saturation, a triode regime,
or a combination of both) but for the sake of building a high
level model we can choose a number proportional to the size of
the gate which produces the same delay as real gate connected
in the same conditions (same load capacitance) as the Excel gate.
-Things get even more complicated for large capacitances or
very fast edges due to the fact that the slew rate will
completely cover any gain effects so the gain might be able to
be replaced with negative infinity which is actually good for us
Static transfer characteristics of two different CMOS inverters with
since it simplifies the model. different size ratios between N and P transistors – (prof. Bruce
<excelunusual.com> McNair – SIT)
3
The Thevenin equivalent (continuation):
– Making abstraction of the input capacitance for now, the
in Rout
equivalent input impedance (resistive) is infinite. out
– The equivalent output resistance could be calibrated by
Vout
benchmarking real transient output waveform (or a precise
G*Vin
Vin – vdd/2
SPICE simulation) with the Excel model for a series of
various size inverters. For now we can consider it somewhere
gnd
in the range 100KW to 500KW..
– The gain for the output level around half the supply
voltage is around -20 (26dB) for a typical modern CMOS
vdd/2
gate, but with the caveat that the equivalent source voltage
needs to be limited between gnd and vdd.
– An equivalent model would be the one below in which the comparator has a gain Gain_comp = G
(about 20) and, of course, its output is limited between “gnd” and “vdd”.
comparator
– Since the gain is fairly high and the input signal has
in large and fast swings around -vdd/2 it might pay off.
(major model simplification and simulation speed
out
+ improvement) to increase the gain of the comparator
Vin Vout to infinity hence replace the comparator with an ideal
inverter.
– An extra argument for adopting this model is the
fact that in realistic transient operation, due to the
fast charging of the output capacitance voltage by the
logic gate, the slew rate effects outweigh the gain
effects (see next page for the simple model) =>>>
<excelunusual.com>
4
A simplified equivalent model:
– We will use the model to the right, which (as we will see soon) can be written as a built-in formula in a single cell without the need to use very slow user
defined functions.
– The problem with this model is that it can simulate rise time and fall time delays but no propagation delays.
In order to simulate propagation delays we Threshold = vdd/2
will need to cascade at least a couple of these models
hence use at the least two cells of formulas.
– The aspect mentioned before is not much of
a problem because as we can see in the
diagram below all the delay in a simple (single-
stage) gate is mainly caused by rise time/fall
time delays (tpLH is about half of the rise time).
A typical diagram explaining the propagation delays and the edge
delays (rise and fall time) for a generic gate
<excelunusual.com>
5
– Looking again at the simulated results of a modern
CMOS inverter (the ones here were published by
professor Bruce McNair from Stevens Institute of
Technology) we can see that, for a sharp input, the
propagation delays are solely caused by edge delays.
– For sloping inputs things might be a little different
but, again the gain of a CMOS gate is high (around –
20) and this must not affect the precision too much.
– Besides, as mentioned before, an approximate model
in Excel could be benchmarked and calibrated against
a precision SPICE simulator if precision is important
and it could be proven that the main contributing
factor in the propagation delay for a simple gate is
the slope delay.
– In the figure to the right there is no practical or
theoretical reason for the output not to start falling at 2ns or start rising at exactly 8ns in time. It
might seems there is if we look at catalog sheets of inverters sold commercially as stand-alone
components (74HC series for instance), but we need not to forget that such parts have several stages (at
least an additional output buffer plus one stage to compensate for the inversion of the buffer in the case
of an inverter).
For registers, counters, etc things are even worse since such parts cannot be made
without using a train of gates. In those cases the edge delay will be the native edge delay of the last stage
(buffer) but the propagation delay will be due to a cumulative effect of the edge delays of the gates in
the critical path. A good example of this concept is a ring oscillator which has an obvious propagation
delay between nonconsecutive stages but the edges of any stage output could be quite sharp.
– The model formulas taking into consideration RC edge delay will be derived in the
next presentation.
to be continued…
<excelunusual.com>
6