Hi Folks, As a kid was fascinated with high power rifles, sniper rifles, cannons and in general, fast projectiles. I’ve been brainwashed with all sorts of urban legends about how far an AK 47 or a pistol can shoot or how thick a steel metal plate a bullet can penetrate at various distances.
I’ve also watched some documentary about snipers and there were talking about highly bent trajectories, how much a bullet looses speed in flight and all that stuff. A lot of those questions in my mind were answered last night while making a “virtual tactical shooting range” in Excel. The nice part about this model is that it takes in consideration the aerodynamic drag with a constant Cx (drag coefficient guessed around 0.25 for a typical military bullet).
You can select the shooting angle, muzzle velocity and you can also choose between eight different standard rounds whose names, weights and diameters I found on the internet: US military M193 Ball, US military M118 Special Ball, Palma Sierra MatchKing, LRBT J40 Match, Sierra MatchKing 7.62, Sierra MatchKing 8.59, LRBT J40 Match and LRBT J40 Match.
Just hit “Fire” after adjusting the aforementioned parameters and you can plot the trajectory and the speed along the trajectory. The plot is auto scaled therefore the visual proportions are not accurate. You can see that a typical bullet has to climb a great deal and loose most of its speed, in order to be able to reach a target say, two miles away.
This model completely changed my perspective on elementary ballistics. Enjoy, George
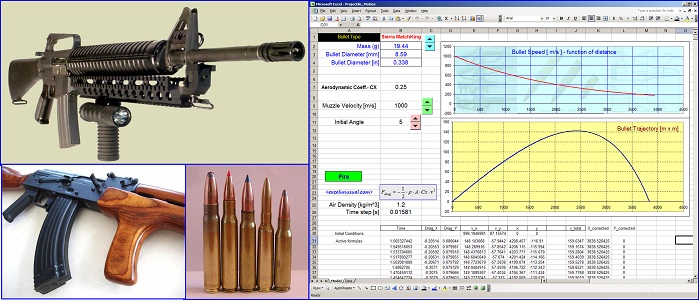

The model neglects a lot of other secondary effects. The purpose of the whole series is to use one (the most important) secondary effect which is plain drag and show how to apply numerical methods to calculate the effects (non parabolic trajectory). While you should not use this model for real shooting calculation but this model will give you a very good idea however of the shape and sag of the trajectory. I don’t believe the angular momentum has any significant effect on the trajectory. That’s just to stabilize the bullet so it does not tumble through the air. If you can tell me why the angular momentum would have any effect on the trajectory I might believe you but I don’t see any reason it would.
This is not an accurate modeling of modern bullet trajectories. Its a fair representation of how a cannon or a musket trajectory would work but this model neglects the effect of the angular momentum imparted by rifling.