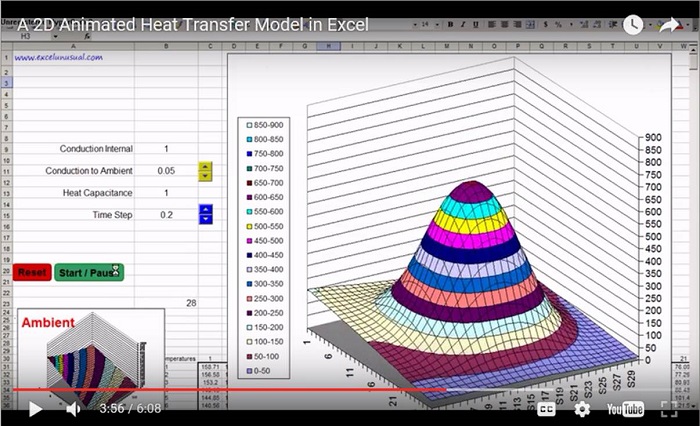
Here is a basic 2D heat transfer model. The first five worksheets model square plates of 30 x 30 elements. The last worksheet is the model of a 50 x 50 plate.
You can modify the initial temperature by hand within the range C21:AF240. It is also a diffusion model. It uses the storage and transport equations derived in the previous tutorials.
The temperature calculations are done all with a single repetitive spreadsheet formula. This is one the easiest models on this blog and a brief tutorial will follow.
On my computer I clocked it at 40 frames/second for the the 30 x 30 models (and 30 fps the 50 x 50 model with Excel 2003) and 1.7 frames/second with Excel 2007. Most of this delay in the 2007 version is due to real time charting.
The intrinsic calculation speed in Excel 2007 (measured with the chart out of view) it’s actually about half the speed of the 2003 version of Excel. I also have a model version using a custom VBA function and it has about half the speed of this one in 2003.
Enjoy, George

Hi George,
It looks real great. However I have some comments;
as an engineer working in practice i’m really missing some units on the constants. Is it SI-units, empirical, or???
Also, a better/clearer description of the time run would be nice.
If you in some way could add an segmented layer of insulation this would really enhance the applicability.
I’m sure these are features you could easily add, and that would certainly make it a very strong tool!
Don’t misunderstand my comments; I think it’s great work!
Regards,
Niels
Hi Neil, sorry for the delay. I am well aware of the units though I left them out in order not to bore the reader. It should be very easy to derive them for yourself using the formulas in the tutorials. Heat is Joules, temperature in Celsius (or Kelvin), mass in Kg and time in seconds. Of course the same units apply for differences. Cheers, George
Really nice!
There is a funny behavior of this algorithm if you set the conductance higher than 1.259 (@ my machine). When the heat is almost equivalent distributed over the plate surface it starts to show some kind of resonance effects: The values of neighboring cells starts to differ stronger and stronger and the overall existing heat (the mean temperature value of all cells) is growing to infinity…
If anyone knows why this occurs (numerical instability, rounding differences etc.), let me know :).
Greetz Chris
Chris, It’s the most elementary numerical scheme. The errors are fairly high. Try to decrease the time step. George
Hey george, could you make some comments on diffusion?
Did you mean using diffusivity as heat conductance as a equivalent?
I will make some comments on that. Give me some a day or two because I stumbled into something.
Diffusivity must be similar to heat conductivity not conductance. Different terms, you can search Wikipedia.
Excellent!That is what I am imagining for. That is really perfect animation! Thanks a lot.
Chang, you are welcome. Download the new model. I removed the custom function and now it’s about twice as fast with just a regular cell formula. 2007 is very slow anyway since the charting is slow. I was able to run 40 frames per second on 2003 with charting and about 300 fps with the chart out of view. The old Excel is a beast. This model is very easy since it does not have all the buttons and is using only ONE temperature calculating function. You spend few minutes to write it in one cell and then just copy-paste it. 3D or ND would be as easy to do as this one. Cheers, George