This is the second part of a tutorial (1, self, 3) describing the creation of an animated Pseudo Random Number Generator model as a Fibonacci type Linear Feedback Shift Register in MS Excel 2003.
This part creates a very simple table type model based on combinatorial logic rather than a sequential type based on registers.
Despite of the fact that this is not the way a real LFSR is built it is useful to go through this tutorial since it will give you more insight into the operation and modeling of such a circuit.
![]()
An Animated Linear Feedback Shift Register (LFSR) as a Pseudo Random Pattern Generator in Excel 2003 – Part#2
by George Lungu
– In the previous section a very sketchy theoretical introduction was given after which the
excel implementation of a 14-bit long Fibonacci type LFSR device was started.
– A device was chosen to generate a maximum length sequence (214-1).
– A “table” type implementation is explored in this section whereas the next section will
contain a “table & sequential” mixed implementation approach.
Some considerations about the spreadsheet “table implementation” of the LFSR:
– The whole model is supposed to be sequential, which means that the present state of the logic is a
function of both the present input and the past inputs (input history). This implies that it has to be an
area in the worksheet allocated to storing past inputs as part of the model.
– As far as implementation is concerned, the whole system could be modeled as a table where the number
of time steps simulated is equal to the number of rows in the table. In other words for each time step we
need to store the information in a table row. This is the easiest way to implement such a system and it
has the advantage of speed (the calculations for all time steps are performed simultaneously by the
worksheet). The disadvantage of this type of implementation is the fact that the table is limited in size to
about 65000 rows in MS Excel 2003. This implies that in the “table” implementation limits the number
of simulated time steps to about 65000 due to worksheet size limitation.
– The hardware equivalent of the “table implementation” is not a sequential circuit but a combinatorial
circuit containing a large number of gates (non inverting buffers) equal to the number of stages in the
shift register times the number of time steps. Of course such a hardware equivalent schematic must
contain the XOR feedback gate group multiplied by the number of modeled time steps.
– The hardware equivalent of the “table implementation” is not a sequential circuit but a
combinatorial circuit containing a large number of gates (non inverting buffers) equal to the number
of stages in the shift register times the number of time steps. Of course such a hardware equivalent
schematic must contain the XOR feedback gate group multiplied by the number of modeled time steps.
A standard schematic of a LFSR:
– We are trying to implement the following sequential schematic:
2 12 13 14 (Out)
FF1 FF2 FF3 FF4 FF5 FF6 FF7 FF8 FF1 FF2 FF3 FF4 FF5 FF6
Clk
– If we are using a table type implementation, the sequential schematic above becomes fully
combinatorial and an example of combinatorial implementation for three (3) time steps is shown
in the next page:
A fully combinatorial schematic for the “table implementation” of the LFSR:
– The schematic below represents a “table implementation” of a four time step model built
in all combinatorial logic. The triangles represent non-inverting buffers.
This models the third time step
This models the second time step
This models the
first time step
This represents the
initial condition set
by the seed value
Input Seed
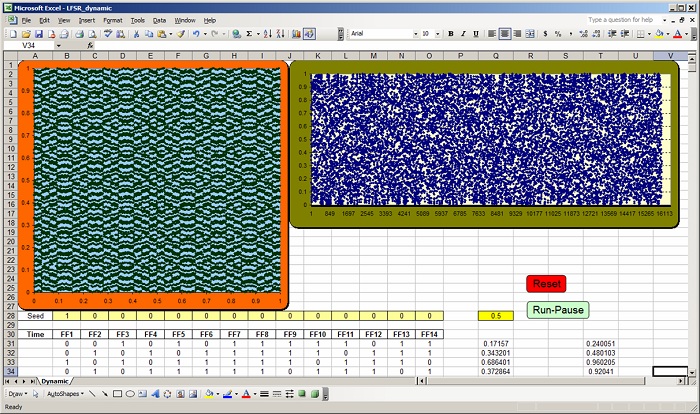
The spreadsheet “table implementation” of the LFSR:
– Rename the first worksheet
“Tutorial_1” and copy it, then
rename the new worksheet
“Tutorial_2” Seed
– A31: “0”, A32: “=A31+1”,
B31: “=B28” then drag-copy
B31 to the right up to cell O31
– A31: “=exor(C31,exor(M31,exor(N31,O31)))”, C32: “=B31” then drag-copy C32to the right up to
cell O32
– Drag-copy range A32:O32 down to row# 14614 (down to range A14614:O14614)
– We can see that range A14614:O14614 contains the starting seed which is what we expect since this
particular LFSR is a maximum length LFSR and it is supposed to repeat the output sequence with a
periodicity of 214-1=16383
Seed
to be continued…