Here is the first part of a tutorial which shows how to build a two dimensional heat transfer model in Excel.
The presentation shows how to partition a square plate in elementary elements on which the simplest form of the heat storage and heat transfer equations can be applied.
The numerical form of the final temperature formula is derived .
![]()
Building a Dynamic Two Dimensional Heat Transfer Model – part #1
by George Lungu
– This is the first half of a tutorial which shows how to build a
basic dynamic heat conduction model of a square plate. The
same principle could be used to model different shape 2D
objects.
– This presentation explains how to partition the plate into
elementary square sections each having four neighboring
elements (right, front, left, back) and each element being
characterized by three parameters: the heat capacitance, the
heat conductance (between neighboring elements) and the
heat conductance with the ambient environment.
– The section also explains how the heat transfer occurs
between the elements by following the two rules of heat
transfer: the storage and the transport equation. The final
numerical temperature calculation formula is derived.
by George Lungu
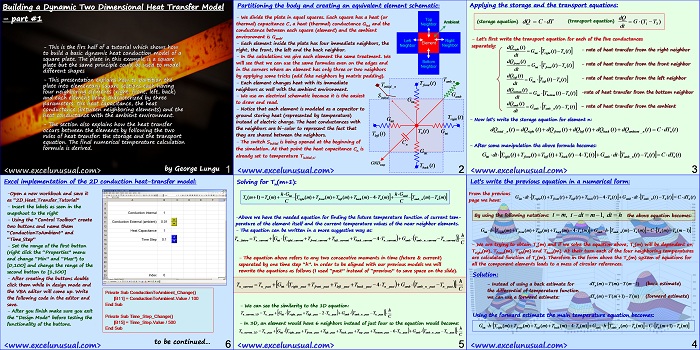
Partitioning the body and creating an equivalent element schematic:
– We divide the plate in equal squares. Each square has a heat (or thermal) capacitance C, a heat (thermal) conductance Gint and the Neighbor
conductance between each square (element) and the ambient environment is Gamb.
– Each element inside the plate has four immediate neighbors, the right, the front, the left and the back neighbor.
– In the calculations we give each element the same treatment. We will see that we can use the same formulas even on the edges and in the corners where an element has only three or two neighbors by applying some tricks (add fake neighbors by matrix padding).
– Each element changes heat with its immediate neighbors as well with the ambient environment.
– We use an electrical schematic because it is the easiest S Gamb to draw and read.
– Notice that each element is modeled as a capacitor to ground storing heat (represented by temperature) instead of electric charge. The heat conductances with
the neighbors are bi-color to represent the fact that they are shared between the neighbors.
– The switch Sinitial is being opened at the beginning of the simulation. At that point the heat capacitance Cn is already set to temperature Tinitial_n.
<excelunusual.com> 2
Applying the storage and the transport equations:
– Let’s first write the transport equation for each of the five conductances separately:
dQ (t)
– rate of heat transfer from the right neighbor
– rate of heat transfer from the front neighbor
– rate of heat transfer from the left neighbor
dt
dQ (t)
bottom
-rate of heat transfer from the bottom neighbor
int bottom n
dt
dQ (t)
amb
– rate of heat transfer from the ambient
amb_n n
dt
– Now let’s write the storage equation for element n:
total_n right front left back ambient_n n
– After some manipulation the above formula becomes:
int right front left back n amb
<excelunusual.com> 3
Let’s write the previous equation in a numerical form:
From the previous page we have:
By using the following notations: t m, t dt m 1, dt h the above equation becomes:
G h T (m)T (m)T (m)T (m)4T (m ) G h T (m)T (m ) C T (m)T (m1)
– We are trying to obtain Tn(m) and if we solve the equation above, Tn(m) will be dependent on
Tright(m), Tfront(m), Tleft(m) and Tback(m). At their turn each of the four neighboring temperatures
are calculated function of Tn(m). Therefore in the form above the Tn(m) system of equations for
all the component elements leads to a mess of circular references.
Solution:
– Instead of using a back estimate for dT (m) T (m) T (m 1) (back estimate)
n
the differential of temperature function
dT (m)T (m1)T(m) (forward estimate)
we can use a forward estimate: n
Using the forward estimate the main temperature equation becomes:
G h T (m)T (m)T (m)T (m)4T (m ) G h T (m)T (m ) C T (m1)T (m)
<excelunusual.com> 4
Solving for Tn(m+1):
-Above we have the needed equation for finding the future temperature function of current temperature of the element itself and the current temperature values of the near neighbor elements.
– The equation can be written in a more suggestive way as:
n future n current int right current front current left current back current n current amb amb n current n current
– The equation above refers to any two consecutive moments in time (future & current)
separated by one time step “h”. In order to be aligned with our previous models we will
rewrite the equations as follows (I used “past” instead of “previous” to save space on the slide).
T T G T T T T 4T G T T
n current n past int right past front past left past back past n past amb amb n past n past
– We can see the similarity to the 1D equation:
T T G T T 2T G T T
n current_1D n past int right past left past n past amb amb n past n past
– In 3D, an element would have 6 neighbors instead of just four so the equation would become:
T T G T T T T T T 6T G T T
n current_2D n past int right past front past left past back past top past bottom past n past amb amb n past n past
<excelunusual.com> 5
Excel implementation of the 2D conduction heat-transfer model:
-Open a new workbook and save it
as “2D_Heat_Transfer_Tutorial”
– Insert the labels as seen in the
snapshoot to the right
– Using the “Control Toolbox” create
two buttons and name them
“ConductionToAmbient” and
“Time_Step”
– Set the range of the first button
(right click the “Properties” menu
and change “Min” and “Max”) to
[0,100] and change the range of the
second button to [1,100]
– After creating the buttons double
click them while in design mode and
the VBA editor will come up. Write
the following code in the editor and
save.
Private Sub ConductionToAmbient_Change()
[B11] = ConductionToAmbient.Value / 100
End Sub
– After you finish make sure you exit the “Design Mode” before testing the functionality of the buttons.
Private Sub Time_Step_Change()
[B15] = Time_Step.Value / 500
End Sub
to be continued…
by George Lungu <excelunusual.com> 6