Most of people have heard of Newton’s second law, mass, moment of inertia or the definition of the acceleration both linear and angular.
The stuff presented here is elementary (9th grade), yet it is generally not properly understood.
What happens when one applies a bunch arbitrary forces on an arbirtarily shaped body?
The resultant force vector produces a linear acceleration while the resultant torque produces a resultant angular acceleration around the center of gravity, both in compliance with Newton’s second law.
The resultant torque can be calculated about an arbitrary point. In this presentation the center of gravity (CG) is chosen as reference for calculating the torque.
![]()
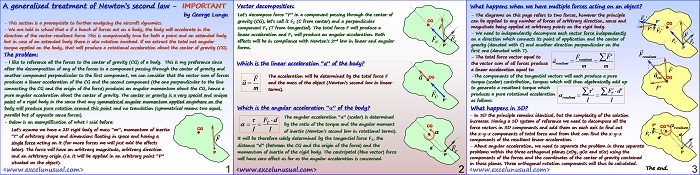
A generalized treatment of Newton’s second law – IMPORTANT
by George Lungu
– This section is a prerequisite to further analyzing the aircraft dynamics.
– We are told in school that a if a bunch of forces act on a body, the body will accelerate in the
direction of the vector resultant force. This is unequivocally true for both a point and an extended body
but in case of an extended body there is also rotation involved. If we extract the total net angular
torque applied on the body, that will produce a rotational acceleration about the center of gravity (CG).
The problem:
– I like to reference all the forces to the center of gravity (CG) of a body. This is my preference since
after the decomposition of any of the forces in a component passing through the center of gravity and
another component perpendicular to the first component, we can consider that the vector sum of forces
produces a linear acceleration of the CG and the second component (the one perpendicular to the line
connecting the CG and the origin of the force) produces a moment of force about the CG, hence a pure
angular acceleration about the center of gravity. The center or gravity is a very special and unique point
of a rigid body in the sense that any symmetrical (couple) moment of forces applied anywhere on the
body will produce pure rotation around this point and no translation (symmetrical means two equal,
parallel but of opposite sense forces).
– Below is an exemplification of what I said before:
Let’s assume we have a 2D rigid body of mass “m”, momentum of inertia
“I” of arbitrary shape and dimensions floating in space and having a
single force acting on it (for more forces we will just add the effects
later). The force will have an arbitrary magnitude, arbitrary direction
and an arbitrary origin (i.e. it will be applied in an arbitrary point “P”
situated on the object).
<excelunusual.com>
Vector decomposition:
Let’s decompose force “F” in a component passing through the center of
gravity (CG), let’s call it FC (C from center) and a perpendicular CG
component FT (T from tangential). The total force F will produce a F
linear acceleration and FT will produce an angular acceleration. Both effects will be in compliance with Newton’s 2nd law in linear and angular C T forms.
Which is the linear acceleration “a” of the body?
The acceleration will be determined by the total force F
and the mass of the object (Newton’s second law in linear terms).
Which is the angular acceleration “a” of the body?
The angular acceleration “a” is determined by the ratio of the torque (moment of force) and I the angular moment of inertia (Newton’s second law
in rotational terms). It will be therefore solely determined by the tangential force FT, the distance “d” (between the CG and the origin of the force) and the momentum of inertia of the rigid body. The centripetal (blue vector)
force will have zero effect as far as the angular acceleration is concerned.
<excelunusual.com>
What happens when we have multiple forces acting on an object?
– The diagrams on this page refers to two forces, however the principle can be applied to any number of forces of arbitrary direction, sense and magnitude being applied at arbitrary points on the rigid body.
– We need to independently decompose each vector force independently on a direction which connects its point of application and the center of gravity (denoted with C) and another direction perpendicular on the first one (denoted with T).
– The total force vector equal to resultant the vector sum of all forces produce resultant
a linear acceleration equal to:
-The components of the tangential vectors will each produce a pure a torque (scalar) contribution, torques which will then algebraically add up to generate a resultant torque which produces a pure rotational acceleration resultant as follows:
What happens in 3D?
– In 3D the principle remains identical, but the complexity of the solution increases. Having a 3D system of reference we need to decompose all the force vectors in 3D components and add them on each axis to find out resultant the x-y-z components of total force and from that can find the components of the resultant linear acceleration.
– About angular acceleration, we need to separate the problem in three separate F
problems within the three orthogonal planes (xOy, yOz and xOz) using the P
components of the forces and the coordinates of the center of gravity contained
in those planes. Three orthogonal rotation components will thus be calculated.
The end.
<excelunusual.com>

