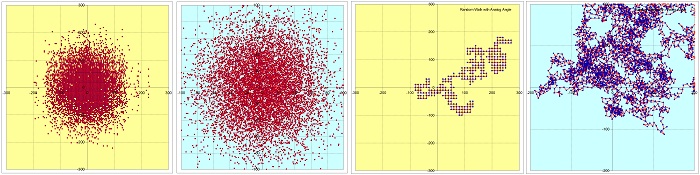
This is a model simulating a two-dimensional random walk in two variants, one by using a digital angle (in 90 degrees increments) and one using an analog angle between zero and 2*pi.
This type of model (similar to the walk of a very drunk man) pertains very well to numerically solving Monte Carlo diffusion type problems.
It is a brute force model using a lot of computer time and resources typically employed when the problem is too complex to be defined and solved by other means. In the case of the “digital angle” a random number is used at each step to evaluate which way the particle will move (classical lattice-confined random walk method).
Depending a random outcome, the particle can at any time move in only four directions (right, forward, left and back). There are four worksheets, containing diffusion animations and plain random walk animations for both digital and analog angles.
[sociallocker]
[/sociallocker]
