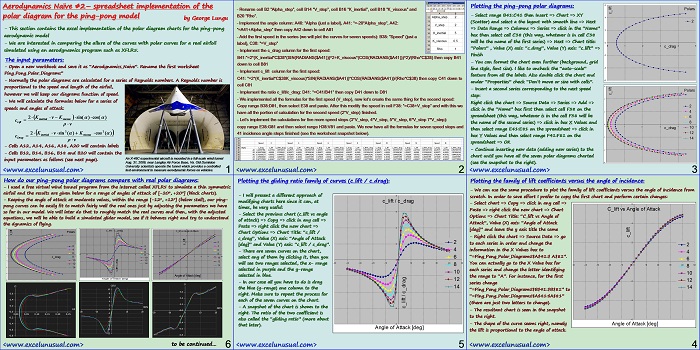
This section of the tutorial implements the lift and drag formulas in a worksheet, creating and charting the polar diagrams for an ultra simplified ping-pong model of an airfoil.
Comparing these diagrams with ones obtained by using a virtual wind tunnel (XFLR5) we can see a decent resemblance for moderate angles of attack (smaller than about 8 degrees in absolute value).
Aerodynamics Naïve #2- spreadsheet implementation of the polar diagram for the ping-pong model
by George Lungu
– This section contains the excel implementation of the polar diagram charts for the ping-pong
aerodynamic model
– We are interested in comparing the allure of the curves with polar curves for a real airfoil
simulated using an aerodynamics program such as XFLR5.
The input parameters:
– Open a new workbook and save it as “Aerodynamics_Naive”. Rename the first worksheet
Ping_Pong_Polar_Diagrams”
– Normally the polar diagrams are calculated for a series of Reynolds numbers. A Reynolds number is
proportional to the speed and length of the airfoil,
however we will keep our diagrams function of speed.
– We will calculate the formulas below for a series of
speeds and angles of attack:
– Cells A12, A14, A16, A18, A20 will contain labels
– Cells B12, B14, B16, B18 and B20 will contain the An X-48C experimental aircraft is mounted in a full-scale wind tunnel
input parameters as follows (see next page).
Aug. 31, 2009, near Langley Air Force Base, Va. Old Dominion
University scientists operate the tunnel which provides a controlled
test environment to measure aerodynamic forces on vehicles.
– Rename cell B2 “Alpha_step”, cell B14 “V_step”, cell B16 “K_inertial”, cell B18 “K_viscous” and
B20 “Rho”.
– Implement the angle column: A40: “Alpha (just a label), A41: “=-20*Alpha_step”, A42:
“=A41+Alpha_step” then copy A42 down to cell A81
– Add the first speed in the series (we will plot the curves for seven speeds): B38: “Speed” (just a
label), C38: “=V_step”
– Implement the c_drag column for the first speed:
B41:“=2*(K_inertial*C$38*(SIN(RADIANS($A41)))^2+K_viscous*(COS(RADIANS($A41)))^2)/(Rho*C$38) then copy B41
down to cell B81
– Implement c_lift column for the first speed:
C41: “=2*(K_inertial*C$38K_viscous)*SIN(RADIANS($A41))*COS(RADIANS($A41))/(Rho*C$38) then copy C41 down to
cell C81
– Implement the ratio c_lift/c_drag: D41: “=C41/B41” then copy D41 down to D81
– We implemented all the formulas for the first speed (V_step), now let’s create the same thing for the second speed:
Copy range B38:D81, then select E38 and paste. After this modify the speed in cell F38: “=C38+V_step” and with this we
have all the portion of calculation for the second speed (2*V_step) finished.
– Let’s implement the calculations for five more speed steps (3*V_step, 4*V_step, 5*V_step, 6*V_step 7*V_step):
copy range E38:G81 and then select range H38:V81 and paste. We now have all the formulas for seven speed steps and
41 incidence angle steps finished (see the worksheet snapshot below).
Plotting the ping-pong polar diagrams:
Polars
– Select range B41:C41 then Insert => Chart => XY
(Scatter) and select a the layout with smooth line => Next 2
=> Data Range => Columns => Series => click in the “Name”
box then select cell C38 (this way, whatever is in cell C38
will be the name of the first series) => Next =>
“Polars” , Value (X) axis: “c_drag”, Value (Y) axis: “c_lift” =>
Finish -2- You can format the chart even further (background, grid
line style, font size). I like to uncheck the “auto-scale” -4
feature from all the labels. Also double click the chart and under “Properties” check “Don’t move or size with cells”.
– Insert a second series corresponding to the next speed
Polars
step:
Right click the chart => Source Data => Series => Add =>
click in the “Name” box first then select cell F38 on the spreadsheet (this way, whatever is in the cell F38 will be the name of the second series) => click in box X Values and 8 then select range E41:E81 on the spreadsheet => click in box Y Values and then select range F41:F81 on the spreadsheet => OK
– Continue inserting new data (adding new series) to the -4 chart until you have all the seven polar diagrams charted
(see the snapshot to the right).
Plotting the family of lift coefficients versus the angle of incidence:
– We can use the same procedure to plot the family of lift coefficients versus the angle of incidence from
scratch. In order to save effort I prefer to copy the first chart and perform certain changes:
– Select chart => Copy => click in any cell => 6
Paste => right click the new chart => Chart C_lift vs Angle of Attack
Options => Chart Title: “C_lift vs Angle of
Attack”, Value (X) axis: “Angle of Attack 4
[deg]” and leave the y axis title the same
– Right click the chart => Source Data => go to each series in order and change the information in the X Values box to
“=Ping_Pong_Polar_Diagrams!$A$41:$ A$81”.
You can actually go to the X Value box for each series and change the letter identifying the range to “A”. For instance, for the first series change
“=Ping_Pong_Polar_Diagrams!$B$41:$B$81” to
“=Ping_Pong_Polar_Diagrams!$A$41:$A$81”
(there are just two letters to change).
– The resultant chart is seen in the snapshot
to the right.
– The shape of the curve seems right, namely
Angle of Attack [deg]
the lift is proportional to the angle of attack.
Plotting the gliding ratio family of curves (c_lift / c_drag):
– I will present a different approach of 8
modifying charts here since it can, at c_lift / c_drag
times, be very useful:
– Select the previous chart (c_lift vs angle
of attack) => Copy => click in any cell =>
Paste => right click the new chart =>
Chart Options => Chart Title: “c_lift /
c_drag”, Value (X) axis: “Angle of Attack
[deg]” and Value (Y) axis: “c_lift / c_drag”.
– There are seven curves on the chart,
select any of them by clicking it, then you will see two ranges selected, the x- range selected in purple and the y-range selected in blue.
– In our case all you have to do is drag the blue (y-range) one column to the right. Make sure to repeat the process for each of the seven curves on the chart.
– A snapshot of the chart is shown to the right. The ratio of the two coefficient is also called the “gliding ratio” (more about that later).
Angle of Attack [deg]
How do our ping-pong polar diagrams compare with real polar diagrams:
– I used a free virtual wind tunnel program from the internet called XFLR5 to simulate a thin symmetric
airfoil and the results are given below for a range of angles of attack of [-20o, +20o] (black charts).
– Keeping the angle of attack at moderate values, within the range [-12o, +12o] (below stall), our ping-
pong curves can be easily fit to match fairly well the real ones just by adjusting the parameters we have
so far in our model. We will later do that to roughly match the real curves and then, with the adjusted
equations, we will be able to build a simulated glider model, see if it behaves right and try to understand
the dynamics of flying.
to be continued…