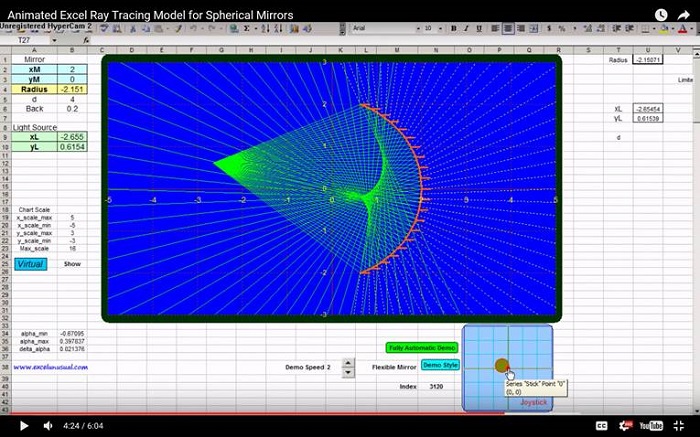
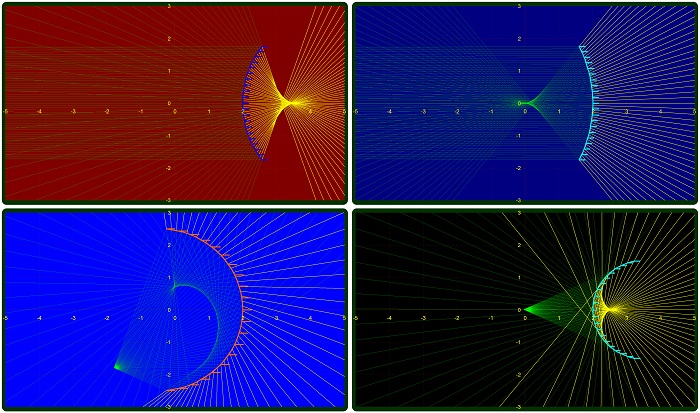
This section explains the illumination setup by using an artificial star, derives the equations of the incident rays and also solves the system of equations for finding the exact coordinates of the points where the incident rays hit the mirror.
Looking at the sign of the determinant of a quadratic equation involved in finding the intersection between an incoming ray and the mirror we can say if the ray hits or misses the mirror, condition later used in a custom VBA reflection function.
Introduction to Geometrical Optics – a 2D ray tracing Excel model for spherical mirrors – Part 2
by George Lungu
– This is a tutorial explaining the creation of an exact 2D ray tracing model for both
spherical concave and spherical convex mirrors.
– While the previous section dealt with creating and plotting the mirror, this section explains
the geometry of the 25-ray light beam emerging from an artificial star „L”.
– This is an exact model in the sense that no geometrical approximations are used, however
the model does not take into consideration diffraction effects.
The input beam parameters:
– There are two variable beam parameters set by the
user: xL and alpha. Parameter yL will be calculated
from xL xM, yM and alpha.
– Essentially we have two points L and M and we write
the slope formula of the segment connecting them (see
the diagram in the next page):
and from here we can derive the formula for yL:
The European Space Agency’s Herschel telescope mirror
(Far InfraRed and SubMillimeter telescope – FIRST)
Create spreadsheet entries for the input
beam parameters in the spreadsheet:
– Range A9:A1 contains labels
– Name call B9 “xL”, name cell B10 “yL” and cell B1 “alpha”
– B10: “=(xL-xM)*TAN(alpha*PI()/180)+yM”
– xL and alpha are input parameters and you can type some constants
in those cells.
Calculating the incidence parameters:
B(xB,yB)
-Let‟s create 25 rays starting from point L y
with the condition that all hit the mirror and
are uniformly spread.
– The first (lowest) ray will hit the mirror at
the lowest extremity (A) and the last one at
the highest extremity (B)
– Based on the above description we can write: alpha
Let‟s express the angle difference between two consecutive rays delta.
We will retrieve the coordinates of points A and B from the mirror table where they were
already calculated B42:C42 and B62:C62
Spreadsheet implementation of the incidence parameters:
– Range A13:A15 contains just labels.
– Name B13 “alpha_min”, B14 “alpha_max” and B15 “delta_alpha”
– B13: “=ATAN((C42-yL)/(B42-xL))
– B14: “=ATAN((C62-yL)/(B62-xL))
– B15: “=(alpha_max-alpha_min)/24”
Writing the equations of the incident rays:
– We have 25 incident rays starting from the artificial star L. In the previous two pages we
derived constraints for the angle of these rays so that they all end up meeting the mirror
surface and covering it uniformly.
– Knowing one point through which all the rays pass ( point L of coordinates (xL,yL) ) and
knowing the angle of each ray with respect to the horizontal x-axis we can write the following
25 equations:
it to a standard line
equation in the x-y plane:
for i=0,1,2,….., 24
Writing the equation of the mirror surface (it‟s actually a curve since it‟s all in 2D):
– We need the mirror surface equation so that forming a system with the previously derived
incident ray equations we can calculate the exact coordinates of the points where the incidence
rays meet the mirror. With that information we can also calculate the slope of the reflected
rays hence being able to write the equations of the reflected rays and chart them.
where (xC, yC) are the
– A standard circle equation
Cartesian coordinates in the x-y plane looks like this:
of the origin
In our case the mirror equation becomes:
Combining the incident ray
equations with the mirror equation M M
we get the following system to solve
to find the incidence coordinates
(intersection points between the
rays and the mirror):
for i=0,1,2,….., 24
Solving the system of equations to find the incidence points:
We have the following system: for i=0,1,2,….., 24
Let‟s substitute the y from the latter equation into the former equation and for now carry just the former equation:
cos (alpha) where a, b, c are given here:
i
The equation becomes:,
This is a quadratic equation whose solution is:
If the determinant: the equation has no solution
In most of cases there are two solutions since a line usually intersects a circle in two points.
Judging by the diagram to the left we can have three conditions:
(a) the ray misses the mirror (no solution to the quadratic (c)
equation – the determinant is negative)
(b) the ray is tangent to the mirror (the determinant is null).
(c) the ray intersects the mirror twice (the determinant is
positive) and we need to choose the higher value (with +) for a
concave mirror (R < 0) and choose the lower value (with
minus in front of the square root) for convex mirrors (R > 0). mirror
Of course in the spreadsheet we need to introduce one more
condition in the function, namely when the ray goes higher
than the upper end of the mirror or lower than the lower end
of the mirror the ray misses the mirror and it passes un-
deviated.
to be continued…