This section explains explains how to implement the formulas that define the emergent (reflected) rays into a custom VBA function.
Though geometrically the last two presentation might look a little elaborate, just be patient and follow the presentation, or even better try to just sneak peek and do it yourself.
All this derivation is done based on first principles and some basic geometry. Take all the time you need, a day, a week or a month, it is worth it and you will be rewarded.
With minor upgrades, this function can later be used to model complex cascaded optical systems.
![]()
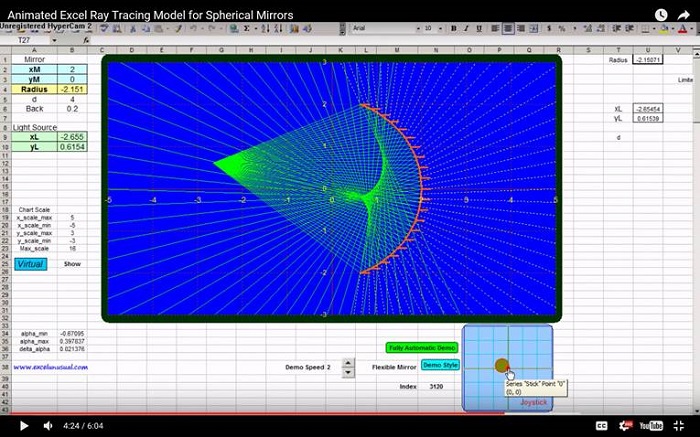
Introduction to Geometrical Optics – a 2D ray tracing Excel model for spherical mirrors – Part 3
by George Lungu
-While the previous section dealt with defining the parameters and geometry of the input
beam and solving the system of equation to find the formulas of the coordinates of the points
where the incident rays meet the mirror, this section creates a VBA custom function to
calculate those coordinates.
– This is an exact model in the sense that no geometrical approximations are used, however
the model does not take into consideration diffraction effects.
Reflect() – new VBA function:
– In the previous section we solved the quadratic
system of equations leading to finding the exact
Cartesian coordinates of the incidence points on the
mirror surface.
– Now we will write a custom VBA function to
implement those results and call it “Reflect”.
– This custom spreadsheet function will return four
numbers: two x-y Cartesian coordinates of the point
in space where the ray hits the mirror surface, the
tangents of the incident angle and emergent angle.
– The next version of this function must be easy to
be cascaded when later used for successive reflection mia nufactured by fusing hexagonal pieces of ULE zero-expansion
glass in a high-temperature furnace.
and refraction models
Review of the formulas behind the “Reflect()” custom function:
The constants a, b, c used in the formulas to the left of the page are defined below:
-Based on the previous presentation if the mirror is convex (R>0) it means we choose the smaller x (the solution with minus) and vice
versa. This is obvious also from the diagram to the right. We can see that the smaller x corresponds to light hitting a convex mirror and
a larger x corresponds to light hitting a concave mirror.
– In this case the formulas become:
Even if there might be solutions determined by the ray intersecting the mirror circle, maybe
the diameter of the mirror “d” will prevent that to happen and the ray will pass undeviated.
We will deal with this situation later and for now let’s implement a preliminary custom VBA
function.
<excelunusual.com>
2
Implementation of a preliminary “Reflect_1()” custom VBA function:
– Let’s implement a preliminary function which has as arguments the Cartesian coordinates
of the light source L (xL, yL), the coordinates of the mirror vertex M (xM, yM), the angle of the
incident ray with respect to the horizontal “alpha_incident” and the mirror radius “R”.
– For now, this function will only return the Cartesian coordinates of the of the point of
incidence I (xI, yI).
– Rename the current worksheet “Tutorial_1+2”
– Copy the current worksheet and rename the copy “Tutorial_3”
– In the VBA editor insert a module and in that module write the following code:
– These are just the formulas from the previous page set up as a custom VBA function.
Function Reflect_1(xL, yL, xM, yM, alpha_incident, R)
Dim a, b, c As Double
-The output of this function is a 2D vector array and we will need to be careful when we type it in (using F2 + Ctrl + c = (xM + R) ^ 2 + (yL – yM – xL * Tan(alpha_incident)) ^ 2 – R ^ 2
Shift + Enter).
a = 1 / Cos(alpha_incident) ^ 2
b = 2 * (Tan(alpha_incident) * (yL – yM – xL * Tan(alpha_incident)) – xM – R)
x = (-b – Sgn(R) * Sqr(b ^ 2 – 4 * a * c)) / (2 * a)
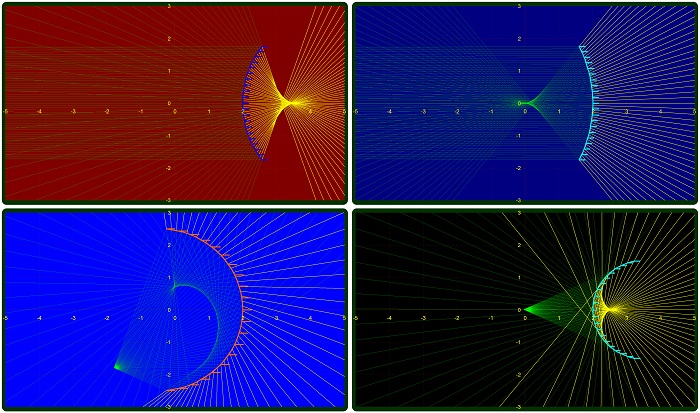
– The correctness of the function will be verified by plotting a series of incident point coordinates on the same chart with the mirror.
y = Tan(alpha_incident) * x + yL – xL * Tan(alpha_incident)
End Function
Reflect_1 = Array(x, y)
Verifying the functionality of the Reflect_1() custom function:
– In the worksheet “Tutorial_3” in the range E42:E66 we will create a “Ray_Index” column
with integer numbers running from 0 to 24. I have chosen a 25 ray input beam since 25 is
different from 21 which is the number of hachure lines on the back of the mirror (I didn’t want
people to inadvertently associate a ray to each hachure dash).
– Cell E42: “=0”, cell E43: “=E42+1”, then copy E43 down to cell E66.
– Cell F24: “=Reflect_1(xL,yL,xM,yM,alpha_min+E42*delta_alpha,Radius)
– Select range F42:G42 and then holding F2 down press Ctrl+Shift+Enter
and you will have the 2D output vector of the custom function in range
F42:G42.
– Copy range F42:G42 down to range F66:G66
– Add a series to the chart having the x-data taken from range F42:F66
and the y-data taken from range G421:G66.
– We can see that the new data (red points in the
snapshot) overlap with the mirror profile and this
is what we intended.
– While deriving the formula I made a small
mistake forgetting the R2 in the formula of “c”. It
took me 2 hours to figure it out and I recommend
that you don’t give up if things don’t work for the
first time. Persist and you will be rewarded!
<excelunusual.com>
4
Deriving the emergent ray angle formulas:
– Emergent rays are the rays leaving the mirror after reflection.
– We need these formulas to write the equations of the emerging rays so that we can plot them.
– We named the center of curvature of the mirror “C” and the incidence point “P”.
– Since C is the center of curvature, the distance CP is equal to the radius of the mirror.
– We also know that the radius of a circle is normal to its circumference.
From the reflection laws we have:
From the diagram we can write
the following angle equality: I
and since triangles CPP’ and LPP” are straight
triangles we can write the following relationships:
from the above
expressions we can
therefore write:
And expressing the
We get the new emergent ray angle as:
emergent ray angle:
We know for every ray and we can calculate p from the coordinate
P M
of point P (which we know too). There is a sign change in front of the
e i
number “2” and it comes from the negative R value in the depicted case:
– Looking at the formula in the previous page we
realize that the sign is correct since for a positive angle the emerging ray climbs.
– Let’s see how to add this formula to the new
“Reflect()” custom VBA function.
Upgrading the “Reflect_1()” custom VBA function to “Reflect()”:
Function Reflect(xL, yL, xM, yM, alpha_incident, R)
Dim a, b, c As Double
– The code to the left
a = 1 / Cos(alpha_incident) ^ 2 creates the new
custom function which
b = 2 * (Tan(alpha_incident) * (yL – yM – xL * Tan(alpha_incident)) – xM – R)
will return not only
c = (xM + R) ^ 2 + (yL – yM – xL * Tan(alpha_incident)) ^ 2 – R ^ 2
the x-y coordinates of
x = (-b – Sgn(R) * Sqr(b ^ 2 – 4 * a * c)) / (2 * a)
the incidence point but
y = Tan(alpha_incident) * x + yL – xL * Tan(alpha_incident) also the slope of the
emergent (reflected
z = alpha_incident + 2 * Application.Asin((y – yM) / R)
ray).
Reflect = Array(x, y, z)
End Function
to be continued…
<excelunusual.com>
6