This section simplifies the formula for the Cartesian coordinates of the terminal point of the reflected ray and derives a very similar formula for a terminal point of the virtual reflected ray.
In the next section all these new formulas together with some old formulas will be combined into a new user defined VBA function which will be used alone to trace the incident, the reflected and the virtual reflected rays.
![]()
Introduction to Geometrical Optics – a 2D ray tracing Excel model for spherical mirrors – Part 6
by George Lungu
– In the previous section we used the custom VBA functions Reflect() and Chart_Reflect() to
calculate the data for the incident and the reflected rays and charted all these rays on the
mirror chart.
– This section simplifies math behind the custom function Chart_Reflect().
– In the next section of the tutorial, the new Chart_Reflect
will be incorporated into a new Reflect_7() custom VBA
function, which in addition calculates a new end point for
the virtual ray. Having the incident point coordinates and
the coordinates of the end point for the virtual ray will
allow us to plot all three types of rays (incident, reflected
and virtual) which is a very useful feature especially for
convex mirrors.
Creating a new Reflect()” custom function:
– Charting line segments determined by two points on 2D
scatter charts seems to be fine even when the points are
out of the visible range (scale) of the chart.
– I had problems though, when one of the points had a
very large coordinate out of the chart scale, case in which
the slope of the line was severely distorted.
A Hubble Space Telescope backup mirror (not flown
into space) of correct shape build by Kodak, on display
<excelunusual.com> at National Air and Space Museum in Washington DC
1
– I encountered the previously mentioned case while plotting the reflected ray.
– Ideally we would like to calculate the exact point where the reflected ray intersects the nearest
border of the visible range on the chart, and make that the end point of the reflected ray.
– After extensive testing I found out that if the end point is farther (even 10-100 times farther
than the length of the diagonal of the visible chart area), things are fine and the reflected ray
still retains the proper slope.
Calculating the end point of the reflected ray- T(xT,yT) the new, simplified method:
– For now, let’s use a the following insight to obtain a second a point for the reflected ray:
Let’s assume the chart has the scale for the x axis ranging between x_scale_min and x_scale_max. Also let’s assume that M(xM,yM) the y axis ranges between y_scale_min and y_scale_max.
– The reflected ray points backwards ( see angle ae) so if we
choose an arbitrary length PT larger than the chart diagonal,
using the definition of the “sine” and “cos” trigonometric functions in the PAT straight triangle we can write:
<excelunusual.com>
2
Deciding a value for the PT length:
We can calculate PT as the diagonal of the viewing area:
The Cartesian coordinates of the terminal point of the virtual reflected ray:
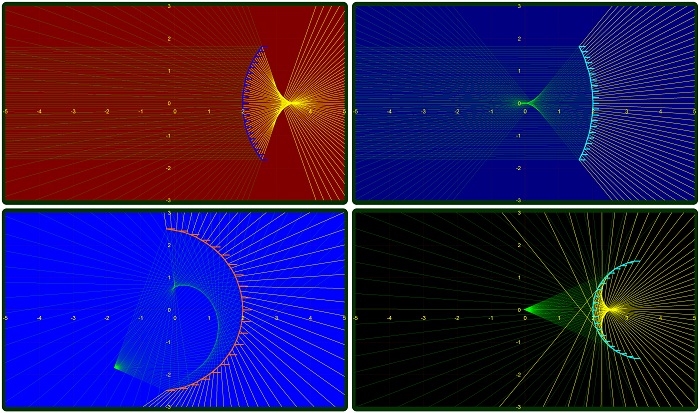
– In certain situations when either the input beam is very
divergent or the mirror is convex, the reflected rays might
be divergent and their extensions (virtual rays) might
converge in a “virtual focus” behind the mirror.
Charting
the virtual rays intersecting themselves in a virtual focus
behind the mirror would be a very convenient way of
assessing optical aberrations in such a mirror.
<excelunusual.com>
3
Calculating the Cartesian coordinates of the the end point of the virtual reflected ray
V(xV,yV):
– Extending the horizontal line that passes through the incidence point and end extending the
reflected ray too, we can see that the reflected and the virtual ray both have the same slope:
T(xT,yT)
a Horizontal (parallel to x-axis)
– The formula for ae was derived before. We can use it to determine the coordinate of the virtual
ray end point which will be very similar to the formulas for calculating the (real) reflected ray
end point:
Next, we will combine all the formulas derived in this section with some of the old formulas into a new Reflect_7 custom VBA function.
to be continued…
<excelunusual.com>
4