This section updates an angle formula so that the virtual glider can now perform both backward and forward loops, as well as inverted flight.
![]()
Longitudinal Aircraft Dynamics #11- 360 full coverage – loops
by George Lungu
– This section fixes an angle issue so that the virtual aircraft will now be able to perform both
backward and forward loops.
Upgrading the model for a full 360 degrees operation – the problem:
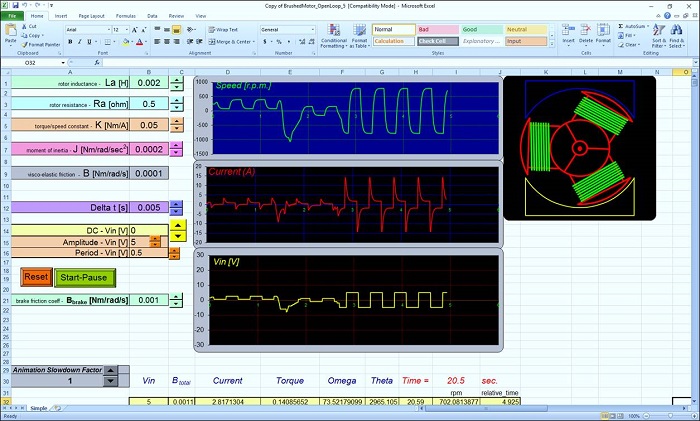
– Using Excel 2003, the speed of the model is decent in actual configuration (50 frames/second on my
PC). In Excel 2007 or 2010 however, the speed is only one tenth of that (5 frames/second).
– We can improve on that later by having the model calculate 10 time steps per iteration by modifying
the macro to copy and paste with an offset of 10 rows. The problem is that we also need to replicate all
the interpolation functions ten times which is quite an editing effort. We will not attempt this task now.
– First let’s copy the last worksheet and rename the copy “Longitudinal_Stability_Model_7”. Don’t forget
to reassign the three control buttons (Reset, Run_Pause and CG_Visibility) the proper macros belonging to
the current worksheet.
– By spending some time with the model I realized that the algorithms stopped working properly (it
generated insanely large numbers) around the point where the aircraft angle touched the 180o or
-180o marks. Using a very small time step I managed to stop the model very close to those points then
manually trying to poke around some cells and see if I was able to pass that point by changing some
values in the worksheet.
– The most important thing I found out was the fact that around those points everything was all right
except that the difference in angle between the aircraft and its speed turned into bogus values. This was
because whereas the aircraft angle was smoothly and continuously being calculated by the numerical
method, the angle of the speed was being assessed by an inverse trigonometric function using the “past”
<excelunusual.com>
speed components calculated by the numerical method.
– Direct trigonometric functions are fine to use at any time regardless of the range of the argument
but I always had problems with the inverse trigonometric functions since they have a limited output
range (arcsine I believe is only defined between -p/2 and p/2). Unless you deal with small angles, you
should stay away from inverse trigonometric functions and prefer using geometry (similar triangles or
right triangles relationships) to calculate anything.
– Going back to our angles, I found out that when the speed angle passed past 180o or -180o, the
difference between this and the aircraft angle suffers big jumps. Since this difference was always small
(usually below 20o) during normal airplane flight I decided to use the cross product between the aircraft
speed vector and the aircraft position vector to figure out the angle over any range.
Angle estimation using the vector cross product:
-A vector, regardless of its orientation, can be univocally represented in a 2D space by two x-y
components. At the same time, the cross product between two vectors can be expressed in two ways,
one is function and the absolute value of the vectors and the sine of the angle between them and the
other is as a pure function of the vector coordinates.
– Let’s refresh our memory about the definition of the vector cross product:
The vector cross product:
The cross product or vector product is a binary operation on two vectors in
three-dimensional space. It results in a vector which is normal to the plane
containing the first two vectors. The sense of the product vector is the sense of
advancement of a right hand screw turned as to overlap the first vector to the
second one on the shortest path. The magnitude is equal to the area of the
parallelogram defined by the two vectors.
<excelunusual.com>
2
– There are two different ways of calculating the vector cross product (where k is the unit vector of
the z-axis):
– From the above equations y x x y we can derive the angle as:
– In our case let’s consider the global system of coordinates. We know plane_ x plane
the angle of the plane as a result of our numerical method scheme
and we can write the components of the plane vector, a vector of u sin( )
plane_ y plane
unit absolute value aligned with the plane:
– We also know the components of the plane v
plane_ x
speed vector derived by the numerical scheme
by integration from the resultant force: v
plane_ y
– Considering that the absolute value of the plane vector was chosen equal to unity, we can
combine the above formulas to find a new expression for the angle between the plane and
the speed of the plane
<excelunusual.com>
3
Worksheet implementation:
– The plane-speed angle difference formula derived on the previous page will be used to calculate the
incidence angle of the wing and horizontal stabilizer. These angles will then determine the resultant
aerodynamic forces and momenta which will then be used to calculate back the airplane speed and
airplane angle.
– We can see that there is a cycle in which the airplane speed and angle are used to calculate themselves.
In order to avoid circular referencing we need to calculate the plane-speed angle difference from the
“past” airplane angle (cell J52) and the “past” airplane speed components (range D52:E52).
– We need to be careful since our angles are expressed in degrees and the trigonometric functions in excel
deal with radians. Also we measure the angles clockwise whereas the standard trigonometric sense in
counterclockwise (the plane angle will be used in the formula with a minus):
– T70: “=180*ASIN((E52*COS(RADIANS(J52))+D52*SIN(RADIANS(J52)))/SQRT(D52^2+E52^2))/PI()”
– We need to do one more thing, and update the formulas for the angle of attack of 30
Plane in upright position performing backward loops the wing and the horizontal stabilizer:
– At this point the model should work fine
with the airplane moving in any direction, Plane in upside down position performing a forward loop
doing back and forward loops equally well.
-Of course the plane can travel from right to left only upright and from left to right -10 -5 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120
only in upside down position. The upper chart has the plane launched at 45 degrees at 25 m/s (upright) with a
wing angle of attack of +3o and stabilizer angle of attack of -8o. The bottom chart starts with the plane launched
the same speed but at -200o with angles of attack of -3o and +9o (most of the flight the plane is inverted).
The end.
<excelunusual.com>
4