This section is dedicated to modeling mechanical systems in Excel 2003 standard.
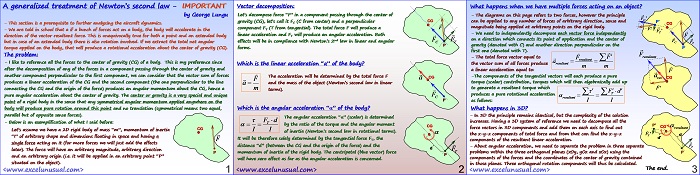
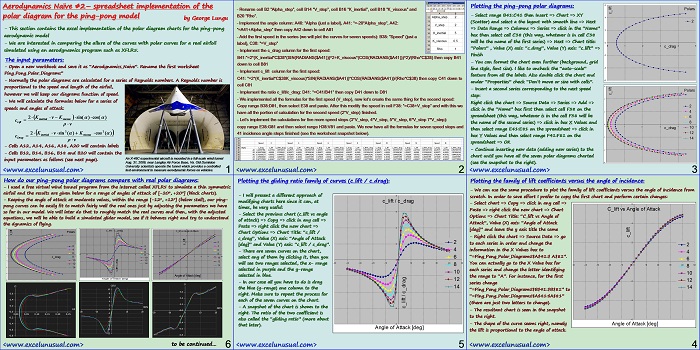
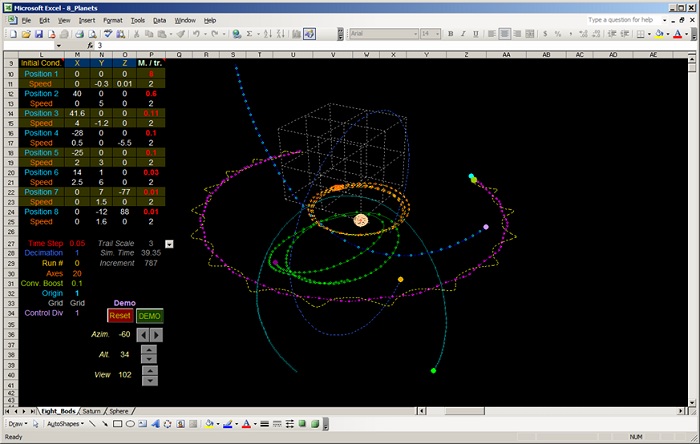
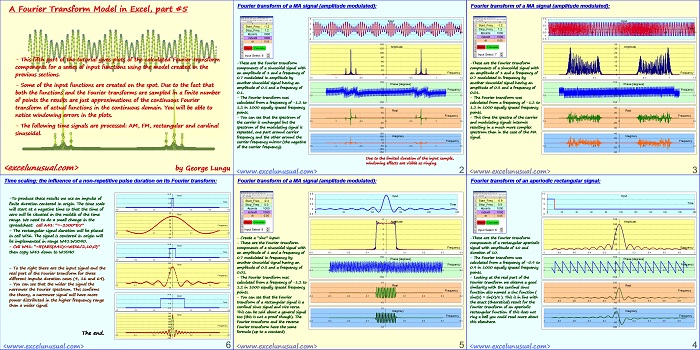
Most of people have heard of Newton’s second law, mass, moment of inertia or the definition of the acceleration both linear and angular. The stuff presented here is elementary (9th grade), yet it is generally not properly understood. What happens when one applies a bunch arbitrary forces on an arbirtarily shaped body? The resultant force vector produces a linear acceleration… Read More... "Newton Generalized Treatment"
This section of the tutorial explains how to create the 2D aircraft components for the animated longitudinal stability model. The first part deals with extracting the x-y coordinates for the fuselage, canopy, vertical stabilizer and rudder. The second part handles the main wing airfoil and the horizontal stabilizer airfoil. All thses parts will be put together in the next section.… Read More... "Longitudinal Aircraft Dynamics #4 – virtual aircraft definition"
This section discusses the layout of the virtual plane and provides for the worksheet implementation of the plane dimensions as input parameters controlled by spin buttons and macros. In the final part a freeform is used to generate raw data for the fuselage. [sociallocker][/sociallocker] Longitudinal Aircraft Dynamics #3- defining the virtual aircraft by George Lungu – This section of the tutorial… Read More... "Longitudinal Aircraft Dynamics #3 – layout parameters and wireframe fuselage generation"
In the previous section, the main wing airfoil and the horizontal stabilizer airfoil were simulated using Xflr5. The three coefficients, lift, drag and moment were then interpolated on charts in Excel using 4th and 5th order polynomials. This section shows a few tricks about how to easily introduce those 60 equations as spreadsheet formulas in Excel ranges. It also presents a simple linear interpolation method across the Reynolds… Read More... "Longitudinal Aircraft Dynamics #2 – 2D polynomial interpolation of parameters cl, cd and cm"
This is a tutorial about using a free aerodynamic modeling package (Xflr5) to simulate two airfoils in 2D (the main wing and the horizontal stabilizer) for ten different Reynolds numbers, then using Excel to extract the approximate polynomial equations of those curves (cl, cd and cm) and based on them, simulate a 2D aircraft as an animated model. This section deals with… Read More... "Longitudinal Aircraft Dynamics #1 – using Xflr5 to model the main wing, the horizontal stabilizer and extracting the polynomial trendlines for cl, cd and cm"
The previous section implemented and charted the ping-pong polar diagrams in a spreadsheet and showed a reasonable similarity, for moderate angles of attack, between these diagrams and the ones modeled using Xflr5, a virtual wind tunnel. This section introduce the concept Reynolds number and it also contains a very brief introduction to Xflr5, the free virtual wind tunnel software. Aerodynamics… Read More... "Aerodynamics Naive #3 – a brief introduction to Xflr5, a virtual wind tunnel"
This section of the tutorial implements the lift and drag formulas in a worksheet, creating and charting the polar diagrams for an ultra simplified ping-pong model of an airfoil. Comparing these diagrams with ones obtained by using a virtual wind tunnel (XFLR5) we can see a decent resemblance for moderate angles of attack (smaller than about 8 degrees in absolute value).… Read More... "Aerodynamics Naive #2 – spreadsheet implementation of the Ping-Pong polar diagrams"
This is the ping-pong aerodynamic analogy. The wing is a ping pong bat and the air is a bunch of evenly spaced array of ping pong balls. It is a naive model but, as we will see in a later post, the polar diagrams derived from this analogy (between -12 to +12 degrees of angle of attack) are surprisingly close shape wise to the real diagrams of a thin,… Read More... "Aerodynamics Naive #1 – deriving the Ping-Pong airfoil polar diagrams"
Have you ever wondered why the flight attendants of a half empty airliner talk people into moving to the front half of the plane? Have you ever wondered why a flying wing can fly without a tail or why the stability of some of these flying wing can be controlled only by computer? Or why a 12 pack stored in at… Read More... "How Do They Fly? – an intuitive look into lift generation and flight stability"
This is an older model of planetary motion in 3D containing eight planets. A video preview can be watched here. [sociallocker][/sociallocker] Read More... "A Legacy 3D Octal Planetary Model"
This part of the tutorial demonstrates the Fourier transform operation in a few cases of periodic and non-periodic signals, such as an AM signal, an FM signal, a rectangular non repetitive signal and a cardinal sine signal. The last slide contains an application to the scaling property of the Fourier transform on a non-repetitive time signal. It actually shows that… Read More... "Spectral Analysis – a Fourier transform tutorial – part #5"
The previous sections explains the creation of a discrete Fourier transform model in Excel. This section and the following one will use the model to calculate and chart the Fourier transform in several cases of periodic and non-periodic signals. [sociallocker][/sociallocker] A Fourier Transform Model in Excel, part #4 by George Lungu – This is a tutorial about the implementation of… Read More... "Spectral Analysis – a Fourier transform tutorial – part #4"
The previous sections of the tutorial handled the basic formulas behind building a Fourier model and creating a set of input functions. This section deals with formula implementation on the spreadsheet, the brief VBA code and the charting of the Fourier transform components. [sociallocker][/sociallocker] A Fourier Transform Model in Excel #3 by George Lungu – This is a tutorial about… Read More... "Spectral Analysis – a Fourier transform tutorial – part #3"
In this tutorial the Excel implementation of a Fourier transform is discussed. Seven input signals are created among which sinusoidal, rectangular and combinations of them. A Dirac impulse, an amplitude modulated (AM) signal and a frequency modulated (FM) signal are also added among the input signal options. [sociallocker][/sociallocker] A Fourier Transform Model in Excel #2 by George Lungu – This is… Read More... "Spectral Analysis – a Fourier transform tutorial – part #2"